Gallery
牛島ラボの Gallery ページへようこそ!
私たちが開発した多相場連成解法 MICS による計算例を動画等とともにご紹介します。
1. 流体中をゆらゆらと落下する固体 (2008)
2. 越流する自由水面流れによる透水堰の破壊 (2006)
3. 自由水面スロッシングと弾性板変形の連成現象 (2008)
4. 自由液面流中の 1,000,000 個の固体運動の連成現象 (2014)
5. 津波に流される240台の車両モデル(防止工あり / なし) (2015)
6. 落下水流による礫(レキ)粒子群の輸送 (2017)
7. 鉛直下方噴流による礫群の輸送 (2019)
8. 底面からの流入水により破壊される粒子層 (2022)
Gallery 別館(近日公開予定です)
流体中をゆらゆらと落下する固体 (2008)
シンプルな流体・固体連成の計算例です。縦長の容器内の流体中を落下していく直方体の固体の動きと周囲の流れを計算します。
身近な現象ですが、ゆらゆらと落下する固体の動きを再現するには、
(1)固体の動きや姿勢の変化による流れの変化と、
(2)変化した流れによる固体運動の再変化、
という相互に影響し合う流体・固体連成を適切に扱うことが必要です。
蛇行しながら落下する固体の運動には、その背後に発生する渦が密接に関係しています。渦付近では流体の圧力が周囲より低くなり、固体の動きや姿勢の変化を引き起こします。私たちの解法 MICS では、物体表面に作用する圧力と粘性応力を体積積分で評価するため、流体が固体におよぼす力とモーメントを容易に計算できるという利点があります。
参考資料: Link to J-STAGE
越流する自由水面流れによる透水堰の破壊 (2006)
実際の河川にも見られる「透水堰」は、自然石や自然素材で作られた、水が流れる間隙がある堰で、environment-friendly な水理構造物といわれます。
水路内にガラス球を積み上げた透水堰(最下層球のみ固定)による実験を行いました。透水堰の上流側(動画の左側)の水位が上昇し、堰を透過および越流する自由水面流れにより、どのように透水堰が破壊されるかを調べました。
計算では、ガラス球は、1個のDEM粒子として扱われます。一方、球の周りの流れは球よりも細かい計算セルにより、高い解像度で計算されます。各ガラス球に働く流体力は、MICS により、運動方程式の圧力項と粘性項の体積積分により求められます。実験との比較の結果、計算結果は実験結果とよく一致することが確認されました。
参考資料: Link to J-STAGE
自由水面スロッシングと弾性板変形の連成現象 (2008)
水を入れた容器に水平加速度を加えると、水面変動を伴う水の揺動(スロッシング)が発生します。
4枚の弾性プレートを底面に固定した容器内でスロッシングを起こす実験を行いました。スロッシングにより、これらのプレートは自由水面変動を伴う流れにより変形しますが、水面変動の大きさはプレートによりいくらか軽減されます。
この現象を MICS により計算しました。弾性プレートは、複数の四面体要素で表現されており、それらの変形は有限要素法(FEM)で計算されます。MICS により得られた流体力を四面体要素の各節点に配分して、弾性プレートの変形を求めています。動画では、流体圧力と関係する渦度ベクトルの大きさ(スカラー量)が、弾性プレートの周辺で大きくなることが示されています。計算結果は実験の状況をほぼ再現していることが確認されています。
参考資料: Link to J-STAGE (水工学論文奨励賞・受賞論文)
自由液面流中の 1,000,000 個の固体運動の連成現象 (2014)
自由液面流中を輸送される多数の任意形状の固体の運動に対する数値実験を行いました。この問題では、流体と固体の力学的な連成現象に加えて、固体と固体が接触する連成現象も扱うことが必要です。
MICS に並列処理を導入してこの現象を計算しました。並列化により、百万個の固体を含む自由液面流れの計算を高速に実行します。並列化には、フラット MPI に基づく領域分割法を利用しました。計算領域内に多数の物体が不均一に分布する場合に、計算負荷がプロセス毎に均等になるように、サブドメイン(青い線で表示)の大きさを計算中に変化させることで、動的負荷分散を試みています。
1つの固体は、121 個の四面体要素で構成されています。この計算では各固体は同一の回転楕円体形状としていますが、固体ごとに異なる形状を設定することが可能です。また、この数値実験では、固体の密度は液体と等しく、中性浮力で浮遊する条件としていますが、固体密度も任意に設定可能です。計算領域全体を示すには、百万個の固体は数が多すぎるため、計算領域全体の一部を動画としています。
参考資料: Link to J-STAGE
津波に流される240台の車両モデル(防止工あり / なし) (2015)
津波が発生すると、沿岸付近の車両が流されるなど、さまざまな漂流物が発生する場合があります。津波による災害に加えて、津波漂流物は深刻な二次被害を引き起こす可能性があります。MICS を利用して、240台の車両モデルが自由水面流れにより浮遊移動する過程の数値実験を行いました。津波漂流物の一部をせき止める円筒状の防止工(Debris Control Structures:以下 DCS)に加えて、地形の影響も考慮できる条件を設定しています。DCS は地表面に固定されています。
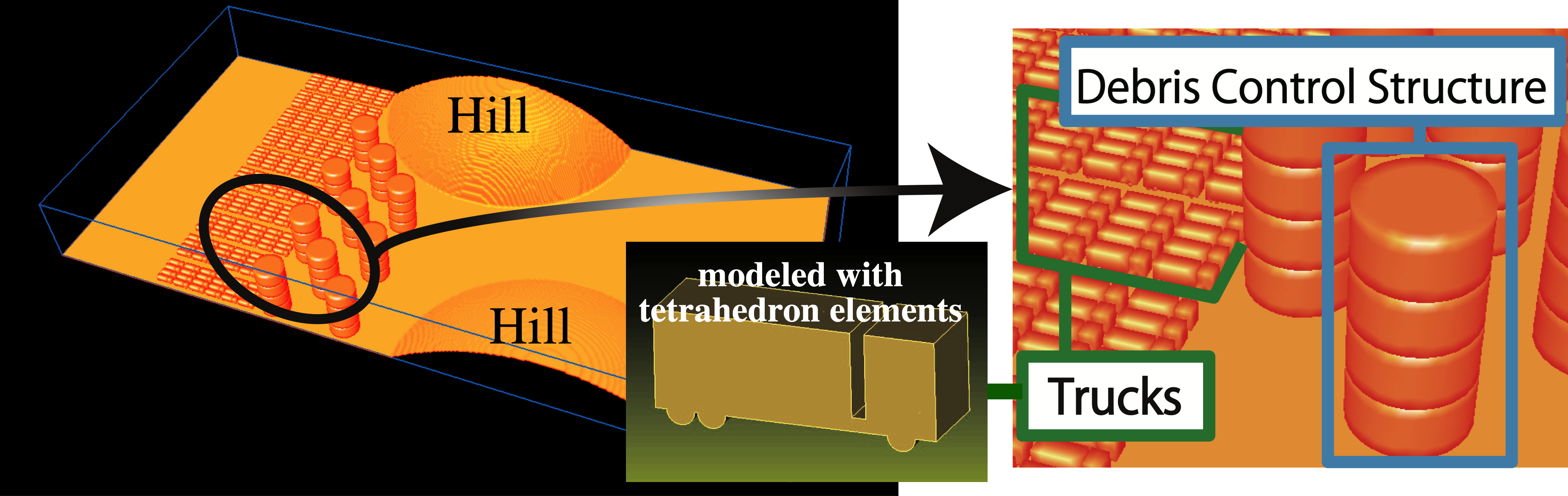
動画では、比較しやすいように、上に DCS なし、下に DCS あり、という条件の計算結果を並べています。地形の影響を考慮できるように、地表面より高い丘を2つ設定しました。
各車両モデルは約 400 個の四面体要素で表現されており、240 台の車両モデルを海岸側(動画の左側)に配置しました。車両モデルの密度は水の密度よりも小さいため、津波流れに浮いた状態で運ばれます。
数値計算は、フラットMPIで並列化されています。動画で車両モデルが輸送される状態を比較すると、DCS により津波漂流物の大部分が捕捉されて、陸側へ流れることを防止する効果があることがわかります。
参考資料: Link to J-STAGE
落下水流による礫(レキ)粒子群の輸送 (2017)
落下水流の着水点付近に礫粒子層があるとき、礫粒子は流れに巻き上げられて移動し、礫層表面は掘り起こされたように窪んでしまうことは、滝が落下する滝壺の様子などから容易に想像できます。この過程を模擬する流体実験を行い、MICS による並列計算結果と比較しました。
長方形の切欠き堰から水流を落下させます。下部に平均粒径約7mm の礫粒子モデルを約16,700個敷き詰めておき、MICS による空気・水・礫粒子群の多相場の並列計算を行いました。
実際の礫粒子の形状を表現するため、約100個の四面体要素で形状を模擬する礫粒子モデルを計算で使用します。26種類の形状を考慮しており、形状ごとに粒子モデルは色づけられています。つまり、約16,700個の粒子群は、26色の粒子から構成されていることになります。
計算結果を可視化する際には、切欠き堰から落下し、着水点で暴れる水流を、密度の等値面で表しています。この等値面の基準密度に満たない水流や、基準を超える気泡などは描画上の理由により表示されていません。
切欠き堰を越流して空気中を落下してくる水流、水流が衝突し巻き上げられる礫粒子群、そして粒子間の接触など、固気液多相が関係する複雑な現象が MICS により再現されました。
流れを止めた後に、掘り起こされた礫層表面の様子を実験結果と比較しました。最大洗掘深さの発生位置は、流下方向に少しずれていましたが、礫層表面の形状や最大洗掘深さは、計算結果とほぼ一致することがわかりました。
参考資料: Link to J-STAGE
鉛直下方噴流による礫群の輸送 (2019)
水理学の分野では、水流により土砂底面が掘り起こされる現象を「洗掘(せんくつ)」とよびます。表面の一部に生ずる洗掘は「局所洗掘」といわれます。
鉛直下方に向かう流速約 1.2 m/s の噴流(小孔から噴出する高速水流)が、礫層上部に衝突して生ずる局所洗掘の計算を行いました。水流と各礫粒子の動きの連成を考慮して、MICS により微細なスケールの局所洗掘現象を再現します。
平均粒径約 7 mm、個数約 16,700 の礫粒子モデルは、26種類の粒子形状から構成され、各形状は四面体要素で模擬されます。1つの礫粒子の大きさに対して約 400 個の流体セルを設定し、粒子周辺の流れを求める大規模な計算を実行しました。京都大学のスーパーコンピュータ( Camphor2:Cray XC40、稼働期間 2016-2022)を利用し、1,088 プロセスの並列計算を行いました(Camphor は 京都大学のエンブレムにあるクスノキです)。
計算結果の動画では、洗掘された礫面形状が見えるように、3次元計算領域の手前(奥行き 160 mm のうち 32 mm まで)の範囲にある礫粒子モデルのみを表示しています。3次元空間中を動く粒子が突然消えたり、現れたりするように見えるのはこのためです。また、動画の水流中では、渦度ベクトルの大きさの等高線を合わせて示しています。
局所洗掘が進行すると、洗掘された礫面付近の粒子は水流による巻き上げや、重力による滑落を続ける一方で、洗掘面の形状がほぼ変化しない平衡状態になります。噴流を止めると、洗掘面付近の粒子は重力により下方へ移動し、洗掘面は水中安息角に近い角度となって礫粒子は静止します。計算では、個々の礫粒子の挙動を追跡できる利点があります。実験結果との比較から、一連の局所洗掘現象が計算で再現されることが確認されています。
参考資料: Link to J-STAGE (応用力学論文賞・受賞論文)
底面からの流入水により破壊される粒子層 (2022)
静止した飽和粒子層に対して、底面の一部から上方に向かう水を流入させます。流入水の流量が大きい場合には、上方に向かう水流は粒子層を貫通して破壊に至ります。
平均粒径約 4 mmの礫粒子とガラス球粒子を使い、水の浸入から粒子層の破壊までの実験結果を計算結果と比較します。
上に示すモノクロ動画は実験の様子を撮影したものです。底面から水を流入させると、流入部付近に空洞(cavity)が発生し、それが大きくなって、粒子層表面に到達して破壊に至ることがわかります。左の礫粒子を使う実験では、貫通した水流がやや蛇行し礫粒子群の動きが左右非対称となること、また礫層上面から粒子が高く飛び出すことなどが観察されます。一方、右の球形ガラス粒子を使う場合には、粒子の動きが穏やかでほぼ左右対称であり、粒子層上面からの飛び出しも比較的低くなりました。同様の実験では、粒子間の過剰間隙水圧の変化も計測し、詳細は参考資料にまとめています。
カラー動画は MICS による計算結果です。奥行き40mmの中央(20mm)断面より手前にある粒子を可視化し、流速ベクトルの大きさを中央断面に描いています(中央断面を横切る粒子は消えたり現れたりします)。礫粒子モデルの個数は約14,300、形状は26種類とし、流体計算セル幅は平均粒径の約 1/10 としました。京都大学のスーパーコンピュータ( Camphor2:Cray XC40、稼働期間 2016-2022)を利用し、1,088プロセス並列計算を行いました。
参考資料: Link to J-STAGE